This article is part of the Beginner Investor Educational Series. To access other articles in this series, please take a look at the menu on the right side of this page (or at the bottom on mobile devices), or start here.

What Is Compound Interest?

Compound interest basically means that interest is also calculated on any previously accrued interest. For example, if you have $10,000 earning 10% interest yearly, then the first year you would gain 10% x $10,000, or $1,000. Your total balance is now $11,000. The following year, you would gain 10% x $11,000, or $1,100. Your total balance is now $12,100. This continues in a snowball effect that exponentially increases the value of this entity.

Time Could Be Your Best Friend

When it comes to compound interest, time could be your best friend... IF you start investing EARLY. The more time time you allow your investments to grow, the more they will compound and earn substantial returns. Many people forego investing for retirement while they are in training, with the rationale of:

"I can start investing when I am an attending."

This is a terrible idea, and I will show you why. I will show you how much future value you are sacrificing by not investing now, using the timeline of my residency and fellowship training as an example. 

I was in training from 2011-2017, which is a 7 year time period in which I was investing as much as I could. For the following example, let's use just the amount that I could put into a Roth IRA. In 2011 and 2012, that was $5,000 per year. From 2013-2017, I could put in $5,500 each. In total, that would be a contribution of $37,500 over 7 years. Assuming an 8% annual rate of return, which is a conservative estimate of the nominal (pre-inflation) rate of return, this is how much this investment will grow, with compound interest:

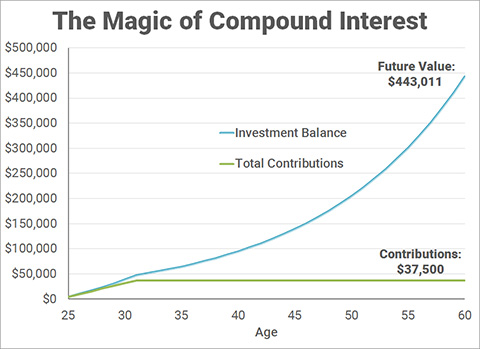
That initial investment of $37,500 can potentially grow to $443,011 by the time I turn 60! As a side note, you can start withdrawing earnings from a Roth IRA tax-free and penalty-free at age 59 1/2, which is why I chose 60 as the endpoint.

How many extra years of working as an attending would you need to make up this amount? That could be maybe 2-3 years. How much extra would you have to save as an attending to make up this amount by age 60? The answer is $4,261 per year for the next 29 years. The total you would need to contribute would be $123,572 instead of just $37,500.

This becomes even more compelling if you include the amount you could invest into your 403(b) or 401(k) account. For me in 2011, the maximum contribution was $16,500. In 2012, it was $17,500. From 2013-2017, it was $18,000 per year. Adding this to the Roth IRA contributions yields a total of $160k contributions over 7 years. With the same 8% growth rate, this is the future value of that investment by the time I turn 60:

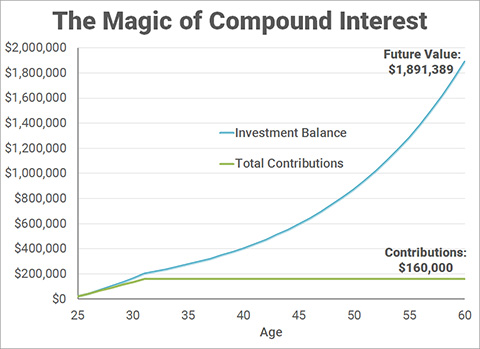
$1.89 MILLION!!! This amount alone is probably sufficient to maintain my lifestyle after I turn 60. That also means that any subsequent savings I have from starting as an attending until the age of 60 could go towards early financial independence. Could it happen in less than 10 years? I hope so! To further convince you, if you deferred this savings 7 years until you became an attending, then you would need to contribute $18,192 per year for the next 29 years to get to $1.89 million. That requires a total contribution of $527,579 instead of just $160,000.

Granted, it will be difficult to max out your retirement accounts while you are in training, unless you moonlight like a boss. The point of this exercise was to illustrate for you the power of compound interest over time. You should invest early, often, and as much as you can to achieve your goals.

Have I convinced you yet? Here are questions you need to ask yourself if you are still hesitant to invest now:

• Are you willing to save an extra 5%-10% as an Attending for the rest of your career to make up for what you didn't save before?
• Can you continue living like a Resident for many years out of training, and put the excess income into investments?

If you answered yes to either of those, then you will probably be fine. Otherwise:

• Are you willing to work past age 60 not because you want to, but because you have to?

Yikes. To that, I say, no thanks.

The long term effects of compounding interest can be hard to imagine, but can be made easier by thinking of the time it takes for an investment to double. The next section will give you a way to quickly calculate investment returns, called the "Rule of 72".

The Rule of 72

The rule of 72 is great for "back of the napkin" math to analyze an investment return. It approximately calculates two things:

1. The # of years it takes an investment to double given the annual compound interest rate.
2. The annual percent rate of return (RoR) of an investment given the amount of time in years that it takes to double.

Here are two practical examples:

1. You bought a house 18 years ago for $100k. Today it is worth $300k. What is the annual rate of return of this purchase?
   • The value of the house has doubled approximately 1.5 times. That gives it a doubling time of 12 years. 72 divided by 12 gives you a RoR of approximately 6%.
   • The true answer is actually 6.29%, but this is a close enough approximation.
2. You currently have $250k invested in the S&P500 index fund. You want to know when this initial investment will break $1 million, given an annual ROR of 8%.
   • The doubling time of this investment is 72 divided by 8, which is 9 years.
   • The investment needs to double twice in order to hit $1 million, which means 2 x 9, or 18 years.

Hopefully, you now understand the power of compound interest. To take advantage of compound interest, you need to start investing RIGHT NOW!